Survey on Digital Signature algorithms
AzamjonAbdullaeva, Mohammed AbdulhakimAl-Absia, AhmedAbdulhakim Al-Absib,
Mangal Sainc, Hoon Jae Leec
aDepartment of Ubiquitous IT, Graduate School, Dongseo University, 47 Jurye-ro, Sasang-gu, Busan 47011,Republic of Korea
b Department of Smart Computing, Kyungdong University 46 4-gil, Bongpo, Gosung, Gangwon-do,
24764, Republic of Korea
c Division of Information and Communication Engineering, Dongseo University, 47 Jurye-ro, Sasang-gu, Busan 47011, Republic of Korea
Azamjon.a.sobirovich@gmail.com, Mohammed.a.absi@gmail.com, absiahmed@kduniv.ac.kr, mangalsain1@gmail.com, hjlee@dongseo.ac.kr
Abstract
Digital signature is a method to provide integrity and authenticity to the digital data signature.in this paper we discuss different types of digital signatures. There are three algorithms that are suitable for digital signature generation under the DSS standard. First one is RSA algorithm second is the ElGamal algorithm, and the tired is Elliptic Curve Digital Signature Algorithm (ECDSA). This paper discusses the cryptography including different types of digital signatures based on the kind of key and a few algorithmsof Digital Signature RSA, EIGamal, and ECDSA.
Keywords: Digital Signature algorithms,elgamal, RSA,ECDSA
1. Introduction
Digital signatures are fundamental in today’s modern world to verify the sender of a document’s identity. A digital signature is performing in the computer as a string of binary. Signature is computer utilizes a set of principles and parameters (algorithm) such that identification of the person signing the document as well as the authenticity of the data can be confirm.
There are three algorithms that are suitable for digital signature generation under the DSS standard. First one is RSA algorithm second is the ElGamal algorithm, and the tired is Elliptic Curve Digital Signature Algorithm (ECDSA) [2]. The hash function is a standard used in the generation signature process. It is used to get a compress version of the data that is called a message digest. To generate the digitally signed message this message digest then put into the digital signature algorithm.Also hash function is used in the verification process. Hash function used in the DSS standard is particular in the Secure Hash Standard (SHS) [1], which are the specifications for the Secure Hash Algorithm (SHA). The SHA is based on principles similar to those used by Professor Ronald L.Rivest of MIT when designing the MD4 message digest algorithm and is closely modeled after that algorithm. When a message of any length < 264 bits is input, the SHA produces a 160-bit output (message digest). Signing the message digest rather than the message often improves the efficiency of the process because the message digest is usually much smaller in size than the message.
2. Simple digital signature algorithm
The public key is used in the signature verification process. The public key need not be kept secret, but its integrity must be maintained. Anyone can verify a correctly signed message using the public key.
Signing Process by Sender: First a message digest (MD) is generated. A message digest is a “summary of the message that is going to be transmitted,” and created by a set of hashing algorithms that were agreed to by both parties. The hashing algorithm ensures the integrity of a message by producing a completely different hash value (MD) when a single piece of the message changes. An MD encrypted with a sender’s private key and an encrypted message digest is created, which is called a digital signature (DS). A digital signature is enclosed with the message and sent to the receiver (Fig. 1).
Signature Verification Process by Receiver: Using the sender’s public key, a receiver decrypts the digital signature to obtain the message digest generated by the sender. Using the same hashing algorithm, the receiver calculates the MD of the received message. The acquired MD value is compared with the sender’s MD value. If they are identical, then the message is not altered and the originality is assured.At this phase, if decrypting the message using the sender’s public key [5] results in a faulty message digests, then the message has been changed and cannot be trusted. However, it is clearly shown that the integrity of the message is maintained but not the privacy, since the message is sent plainly.
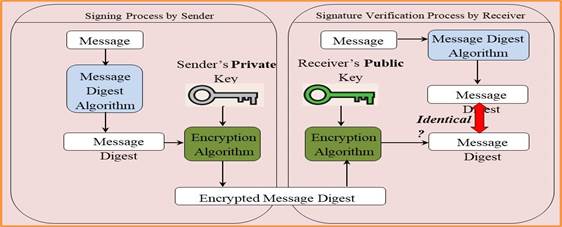
Fig. 1Simple digital signature algorithm
This may be suited to a situation where confidentiality is not an issue. In order to ensure confidentiality in communication, the message should be encrypted. Basically, a digital signature scheme typically consists of three algorithms, namely key generation, signing and signature-verifying algorithms. The techniques are varied, and these systems are categorized based on their mathematical problems. Generally, public key systems are grouped into three main classes which are based on integer factorization (i.e. RSA), discrete logarithm (i.e. DSA), and elliptic curve discrete logarithm (i.e. ECDSA). The security degrees of all the techniques are based on the hardness of mathematical problems.
3. Digital Signature Algorithm (DSA)
The
DSA can be viewed as a variant of the ElGamal signature scheme[3]. Its security
is based on the intractability of the discrete logarithm problem in prime-order
subgroups of![]() .
.
DSA domain parameter generation. Domain parameters are generated f or each entity in a particular security domain. (See also the note below on secure generation of parameters.)
Select a 160-bit prime D and a 1024-bit prime b with property that D | b-1.
(Select
a generator g of the unique cyclic group of order Din![]() .) Select an element h
.) Select an element h![]() and compute g=
and compute g=![]() mod b (Repeat until
mod b (Repeat until ![]() )
)
Domain parameters are b, D and g;
DSA Key Pair Generation. Each entity A in the domain with domain parameters (b, D, g) does the following:
Select
random or pseudorandom integer x such that![]() .
.
Compute y=gx mod b.
A’s public key is y; A’s private key is x.
DSA Signature Generation. To sign a message m, A does the following:
Select
a random or pseudorandom integer k, ![]() .
.
Compute X= gk mod b and r=X mod D. If r=0 than go to step 1.
Compute k -1mod D.
Compute e=SHA-1(m).; Compute s= k -1{e + xr} mod D. If s=0 then go to step 1.
A’s signature for the message m is (r,s).
DSA Signature Verification. To verify A’s signature (r,s) on m. B obtains authentic copies A’s domain parametres (b, D, g) and public key y and does the following:
Verfy that r and s are integers in the interval [1, D-1].
Compute e=SHA-1(m); Compute w= s -1mod D.
Compute u1=ew mod D and u1=rw mod D.
Compute
X= ![]() mod b and v=X mod D.
mod b and v=X mod D.
Accept the signature if and only if v=r.
4. Digital Signature Algorithm (RSA)
RSA is a public-key cryptosystem that gets its name from its inventors – Rivest, Shamir and Adleman and was developed in 1977[4]. It has since withstood years of extensive cryptanalysis. It is used for electronic commerce and many other secure communications over the Internet. RSA is a Block cipher in which the plain text and cipher text are integers between 0 and n – 1 for some integer n. RSA gets its security from the difficulty of factoring large numbers.
Working of RSA: Select 2 random large prime numbers b and D of almost equal length. Compute their product n = bD. The Euler’s Totient function f(n) is computed, i.e. f(n) = (b – 1)(D – 1). We then choose two keys a and b such that, a.b º 1 (mod f(n)). One of the keys say a is made public while the other key b is kept a secret. At this point, we no more require b, D and f(n). We can discard these values. If we have a message M, encryption of M is C = Ma mod n, C is the resultant cipher text. Decryption of C is achieved by M’ = Cb mod n.
Consider M’ = Mab mod n = Mkf(n) + 1 mod n (Since a.b º 1 (mod f(n))) Þ M’ = M . Mkf(n) mod n = M mod n (It can be proved that xf(n) º 1 (mod n))
Hence we see that M = M’. Thus we have achieved efficient encryption and decryption using RSA.
5. Elliptic Curve Digital Signature Algorithm (ECDSA)
ECDSA Key Generation. The user A follows these steps where p is a large prime:
Select a random integer d ∈[1, S - 1].
Compute D = d x b.
The public and private keys of the user A are D and d, respectively.
The other parties can check if the public key is valid by;
Checking that D ≠ 0.
Checking that xD and yD are properly represented elements of FD.
Checking that D is on the elliptic curve defined by a and b.
Checking that sD = D.
If any of these checks fail the public key D is invalid, otherwise D is valid. The following procedure describes how to generate the signature.
ECDSA Signature Generation
Select a pseudorandom integer k ∈[1, s - 1].
Compute k x B = (x1, y1) and r = x1 mod s.
If x1 ∈, GF(2k), it is assumed that x1 is represented as a binary number.
If r = 0 then go to Step 1.Compute k-1 mod s.
Compute s = k-1(H(m) + d • r) mod s.
Here H is the secure hash algorithm SHA-1.
If s = 0 go to Step 1.
The signature for the message m is the pair of integers (r, s).
ECDSA Signature Verification
Verify that r and s are integers in the interval [1,s-1].
Compute c = s-1 mod s and H(m).
Compute u1 = H(m) • c mod s and u2 = r • c mod s.
Compute u1 x B + u2 x D = (x0, y0) and v = x0 mod s
Accept the signature if v = r.
ElGamal Digital Signature
El Gamal Key Generation
The
prime b, a generator g of field![]() , A's private key dA is a random integer
from the interval [1; b-1] and her public key is yA =
, A's private key dA is a random integer
from the interval [1; b-1] and her public key is yA = ![]() mod b.
mod b.
6. El Gamal Signature Generation
Select a random integer k from interval [1; b-1], satisfying gcd(k; b-1) = 1;
Compute k -1mod (b-1);Compute r = gk mod b;
Compute
s = k-1{h(m) - dAr} mod (b-1). h is the hash function:{0; 1}![]() Zb.
Zb.
(r; s) is A's signature of message m.
El Gamal Signature Verification
Verify
that 1 ![]() r
r ![]() b - 1;Compute v1 =
b - 1;Compute v1 =![]() gk mod b;
gk mod b;
Compute h(m) and v2 = gh(m);Accept if and only if v1 = v2.
Scour Digital Signature; Scour Key Generation
Primes
d, b, satisfying d | (b-1), the generator ![]() of
the unique cyclic ubgroup of
of
the unique cyclic ubgroup of ![]() (satisfying
(satisfying ![]() u
u ![]() ,
, ![]() =u(b-1)/d
mod b, but
=u(b-1)/d
mod b, but ![]() 1). A's private key dA is a random
integer from the interval [1; d-1], and her public key is yA =
1). A's private key dA is a random
integer from the interval [1; d-1], and her public key is yA = ![]() mod b; Schnorr Signature Generation
mod b; Schnorr Signature Generation
Select a random integer k from interval [1; d-1];
Compute
r = ![]() k mod
b, e = h(m || r) and s = dAe + k mod d. h is the hash function {0; 1}
k mod
b, e = h(m || r) and s = dAe + k mod d. h is the hash function {0; 1}![]() Zd. (s ; e) is A's signature of message
m.
Zd. (s ; e) is A's signature of message
m.
Schnorr Signature Verification
Compute
v =![]() s
s![]() mod b and e'= h(m || v);
mod b and e'= h(m || v);
Accept if and only if e = e';
7. Conclusion
The DSA was proposed in August 1991 by the U.S. National Institute of Standards and Technology (NIST) and was specified in a U.S. Government Federal Information Processing Standard (FIPS 186) called the Digital Signature Standard (DSS). In this paper we perused the concept of Cryptography including different types of digital signatures based on the kind of key and a few algorithms first one is RSA algorithm, second is the ElGamal algorithm, and the tired is Elliptic Curve Digital Signature Algorithm (ECDSA). Future work would consider the Comparison of Security Levels for RSA algorithm, ElGamal algorithm, and Elliptic Curve Digital Signature Algorithm.
Acknowledgment
This work was supported by Institute for Information and Communications Technology Promotion(IITP) grant funded by the Korea government(MSIT) (No.2018-0-00285)
References
[1] Digital Signature Algorithm Based on Hash Round Function and Self-certified Public Key System by Chen Hai-peng, Shen Xuan-jing, Wei Wei, 2009 First International Workshop on Education Technology and Computer Science.
[2]G. Agnew, R. Mullin and S. Vanstone, "An implementation of elliptic curve cryptosystems over 2155 ", IEEE Journal on Selected Areas in Communications, 11 (1993), 804-813.
[3]Digital signature signing engine to protect the integrity of digital assets by Gordon W. Romney, 1-4244-0406- 1/06/$20.00 ©2006 IEEE.
[4] A New Efficient Digital Signature Scheme Algorithm based on Block cipher by Prakash Kuppuswamy, Peer Mohammad Appa,Dr. Saeed Q Y Al-Khalidi, IOSR Journal of Computer Engineering (IOSRJCE) ISSN: 2278-0661, ISBN: 2278-8727Volume 7, Issue 1 (Nov. - Dec. 2012), PP 47-52
[5] Rivest,R.L.,Shamir,A.,and Adleman,L.,” A method of obtaining Digital Signatures and Public key cryptosystems”,Comm.ACM,21,1978.